![]()
Dr. Liu's research interests are in computational mechanics, especially modeling of advanced materials (including composites, nanomaterials, biomaterials and MEMS) and wave propagation problems (acoustic and elastic waves). He has been focusing on large-scale modeling of materials/devices at the micro-length scale for which the continuum mechanics based approaches can be employed. He is specialized in the boundary element method (BEM), for which he has devoted his research efforts for more than 30 years.
The BEM is a numerical method for solving boundary integral equations (BIE) (Fig. 1. See also An Introduction to the BEM, updated 10/16/2025). In the BEM, only the boundary of a problem domain is discretized using surface elements for 3-D problems or line elements for 2-D problems. Therefore, it can save a great deal of efforts in the modeling stage for problems with complicated geometries or in infinite domains. In recent years, the computational efficiencies of the BEM solutions have also been improved dramatically by the so-called fast multipole method (FMM). Both the CPU time and memory requirement of the fast multipole BEM (FMBEM or fast BEM) can be reduced to O(N). This has brought about numerous new applications for the BEM in applied mechanics and engineering.
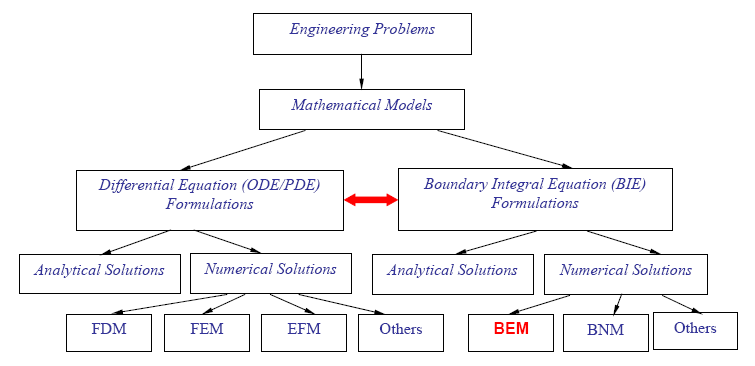
Figure 1. The BEM relative to other numerical methods in
computational mechanics (the red double-headed arrow indicates that the PDE and
BIE formulations are mathematically equivalent).
Dr. Liu and his group have been working on the fast
multipole BEM and pushing its applications in different engineering fields in
the last 20 years. His group has developed new
FastBEM Software for solving 2-D/3-D potential (including electrostatics), 2-D/3-D elasticity,
2-D/3-D Stokes flow, and 2-D/3-D acoustic wave problems. Some examples on the fast multipole BEM for solving various large-scale
problems in applied mechanics are presented below to demonstrate the advantages and
huge potentials of the fast multipole BEM.
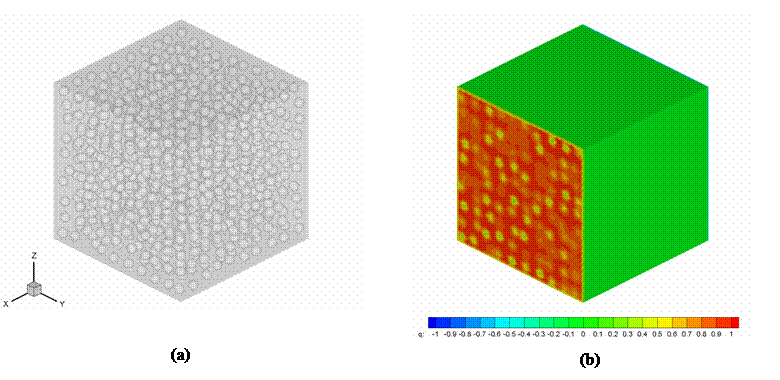
Figure 2. (a) A porous material model with 1,000
spherical voids; and (b) the computed heat flux.
Figure 2 (a) shows a model of a
porous material with voids for thermal analysis. The model contains 1,000
randomly distributed spherical voids and is applied with a linear temperature
field in the x-direction and zero flux on all other surfaces (including the
surfaces of the voids). A total of 558,000 triangular constant boundary
elements were used to discretize all the surfaces of this model and the model was
solved on an old laptop PC with 512 MB RAM. The computed heat flux on surfaces
normal to the x-axis is shown in Fig. 2 (b), which can be averaged and used to
estimate the effective thermal conductivity of this porous material.

Figure 3.
Modeling of scaffolds: (a) Fabricated scaffolds; (b) deformation computed
with the fast multipole BEM.
Figure 3 shows a stress analysis of
scaffolds using the fast multipole BEM. Scaffolds are engineered biomaterials used for
growing tissues. The geometries (Fig. 3 (a)) of scaffolds are complicated and
present great challenges for domain-based methods for the analysis. For a fast
multipole BEM model, 267,588 surface elements were employed and the total DOFs
(degrees of freedom) were 802,764. The model was solved successfully
on a laptop PC with 1 GB RAM. The computed deformation (Fig. 3 (b)) under
tension in the z-direction can be employed to estimate the effective stiffness.

(a) (b)
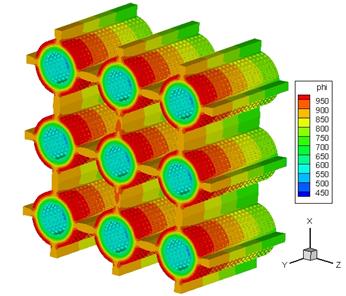
Figure 4. Fuel cell stack model:
(a) 3x3 stack model; (b) computed temperature distribution.
Figure 4 (a) shows a solid oxide fuel cell (SOFC) model with nine cells used for thermal analysis. There are 1,000 small holes on the inner and outer surfaces of each cylindrical cell, with a total of 9,000 holes for the entire stack model! Due to the extremely complicated geometries, the FEM (such as ANSYS) can only model one cell on a PC with 1 GB RAM. For the fast multipole BEM, however, multi-cell models can be handled readily, such as the 9-cell stack modeled successfully with 530,230 boundary elements and solved on the same PC with 1 GB RAM (Fig. 4 (b)).
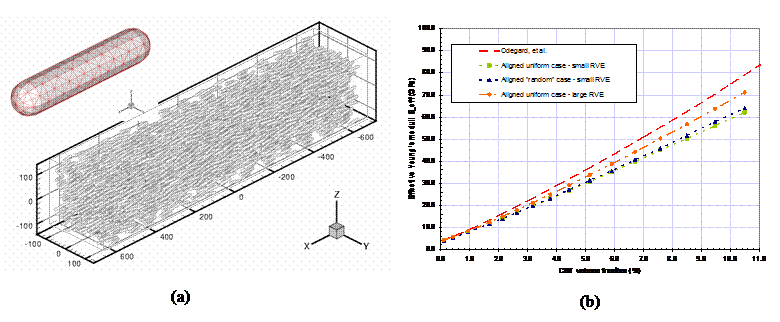
Figure 5. (a) An RVE for a CNT composite using the fast multipole
BEM
(insert shows the mesh on the CNT fibers); (b) Computed effective moduli
as compared with the MD results (by Odegard, et al., 2003).
Figure 5 (a) shows a representative
volume element (RVE) of a CNT/polymer composite with 2,197 CNT fibers modeled
with 3,018,678 DOFs. The RVE is loaded in the x-direction in order to evaluate
the effective modulus in that direction. Only surface elements are needed on
the boundaries and interfaces with the BEM. The largest RVE studied so far
contains 16,000 CNT fibers modeled as rigid inclusions in a polymer and with
perfect bonding interfaces. The total DOFs modeled so far are above 28 millions
with the fast multipole BEM and the model was solved on a supercomputer at Kyoto University.
The extracted effective Young’s moduli (Fig. 5 (b)) from such models are very
close to the result obtained by Odegard, et al.
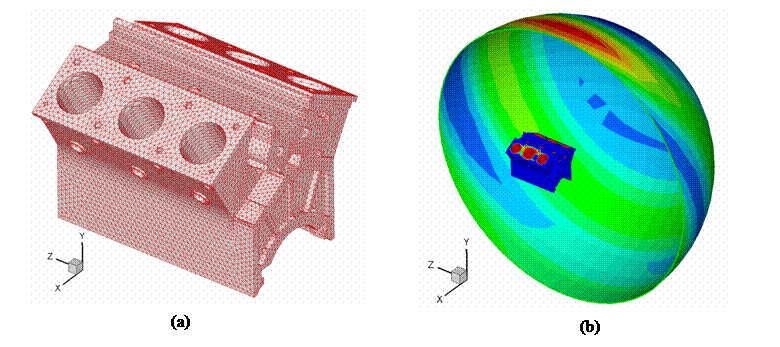
Figure 6. (a) An engine block BEM model; (b) Computed radiated acoustic pressure using the fast multipole BEM.
Figure 6 (a) shows an engine block model with the BEM mesh for acoustic analysis. Point sources are placed at each of the six cylinders to simulate the noise sources of the engine in operation. The radiated waves are computed on the engine surface and on a data collection surface in semispherical shape and some distance way from the engine model (Fig. 6 (b)). A total of 37,482 boundary elements are used for this analysis, with the non-dimensional wave number ka = 3.5. The total CPU time used is about 4,500 seconds on a laptop PC with an Intel 1.6 GHz Centrino processor and 512 MB RAM.
All the above examples show that the fast multipole BEM can be a very effective and efficient numerical tool for modeling and analyzing various advanced materials, such as porous materials, biomaterials, and nanocomposites, as well as structures or devices with complicated geometries, such as fuel cells, engine blocks and MEMS. Large-scale models with unprecedented details and total DOFs above one million can be solved now readily on a desktop PC with 1 GB RAM, and billions of DOFs on a supercomputer (which would require one to solve one billion DOFs on a PC, and hundreds of trillions of DOFs on a supercomputer, respectively, with domain based methods).
If you are interested in Dr. Liu's research, please continue to browse other sections (Publications,
FastBEM Software,
etc.) of this website and feel free to contact Dr. Liu to ask for more
information.
![]()
Last Updated: October 17, 2025